sábado, 25 de septiembre de 2010

AXIOMAS DE LA PROBABILIDAD

PROBABILIDAD

En ocasiones cuando se habla de probabilidad o posibilidad de que un evento ocurra, se pierde la credibilidad acerca del evento en cuestión, pero ¿es posible tener siempre la certeza total en todo proyecto o actividad que se desea realizar?, es muy difícil tenerla, debido a que el llevar a efecto un proyecto cualquiera por más simple que este sea, éste está sujeto a una gran diversidad de factores que afectan su ocurrencia, ¿entonces que es lo más aconsejable para predecir su ocurrencia?, la probabilidad es la que nos ayuda en estos casos, ya que basándose en estadísticas, podemos cuantificar la posibilidad de ocurrencia de los eventos y por consiguiente tomar una buena decisión basados en esta información.

CONCEPTO.

La probabilidad se encarga de evaluar todas aquellas actividades en donde se tiene incertidumbre acerca de los resultados que se pueden esperar, esto quiere decir que la probabilidad está presente en casi en todas las actividades que se pretenda realizar, ejemplos:

-Cualquier proyecto de Ingeniería o de otras áreas

-Competencias deportivas

-Juegos de azar, etc., etc.

¿Cómo podemos calcular probabilidades?

1. Haciendo uso de las estadísticas.

En este caso, se hace uso de la información que se ha acumulado acerca del evento que nos interesa, y después de esto se procede a calcular las probabilidades requeridas.

Ejemplo. Determine la probabilidad de que en cierta línea de producción se manufacture un producto defectuoso, si se toma como referencia que la producción de la última semana en esta línea fue de 1,500 productos, entre los que se encontraron 8 productos defectuosos.

p(producto defectuoso) = No de productos defectuoso /Total de productos producidos en la semana

= 18 / 1500 = 0.012

Lo anterior nos indica que es muy probable que 1.2 productos de cada 100 que se manufacturen en esa línea serán defectuosos.

¿Porqué se utilizó para calcular las probabilidades la información de la semana inmediata anterior?. Debido a que esta refleja la situación que guarda actualmente la producción de la línea mencionada.

2. Basándose en la experimentación. Hay casos en los que después de repetir un número muy grande de veces un experimento, es posible determinar las probabilidades de ocurrencia de algunos eventos, tales como: La probabilidad de que aparezca águila al lanzar una moneda equilibrada, la probabilidad de que aparezca el número 3 en un dado, etc., etc.

Ejemplos:

p(águila) =1/2 = 0.5

p(aparezca el número 3)= 1 / 6 = 0.1666

AXIOMAS Y TEOREMA

AXIOMAS

Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función definida sobre un conjunto de sucesos determine consistentemente sus probabilidades. Fueron formulados por Kolmogórov en 1933.

Dado un conjunto de sucesos elementales, Ω, sobre el que se ha definida una σ-álgebra (léase sigma-álgebra) σ de subconjuntos de Ω y una función P que asigna valores reales a los miembros de σ, a los que denominamos "sucesos", se dice que P es una probabilidad sobre (Ω,σ) si se cumplen los siguientes tres axiomas.

Primer axioma

La probabilidad de un suceso

A

es un número real mayor o igual que 0.

$P(A) \geq 0$

Segundo axioma

La probabilidad del total,

Ω

, es igual a 1, es decir,

$P(\Omega) = 1\!$

Tercer axioma

Si $A_1, A_2, \dots$ son sucesos mutuamente excluyentes (incompatibles dos a dos, disjuntos o de intersección vacía dos a dos), entonces:

$P(A_1 \cup A_2 \cup \cdots) = \sum P(A_i)$ .

Según este axioma se puede calcular la probabilidad de un suceso compuesto de varias alternativas mutuamente excluyentes sumando las probabilidades de sus componentes.

En términos más formales, una probabilidad es una medida sobre una σ-álgebra de subconjuntos del espacio muestral, siendo los subconjuntos miembros de la σ-álgebra los sucesos y definida de tal manera que la medida del total sea 1. Tal medida, gracias a su definición matemática, verifica igualmente los tres axiomas de Kolmogórov. A la terna formada por el espacio muestral, la σ-álgebra y la función de probabilidad se la denomina Espacio probabilístico, esto es, un "espacio de sucesos" (el espacio muestral) en el que se han definido los posibles sucesos a considerar (la σ-álgebra) y la probabilidad de cada suceso (la función de probabilidad).

Propiedades que se deducen de los axiomas

De los axiomas anteriores se deducen otras propiedades de la probabilidad:

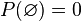$P(\varnothing)=0$ donde el conjunto vacío $(\varnothing)$ representa en probabilidad el suceso imposible
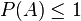
Para cualquier suceso $P(A) \leq 1$
$P(A^c)=1-P(A)\;\!$
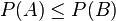
Si $A \subseteq B$ entonces $P(A) \leq P(B)$
$P(A \cup B)= P(A) + P(B) - P(A \cap B)$

Ejemplos

Como ejemplo se puede tomar como espacio muestral a los posibles resultados al arrojar un dado corriente $\Omega = \left \{ 1, 2, 3, 4, 5, 6 \right \}$ , tomaremos como σ-álgebra todos los subconjuntos posibles de Ω (que en matemáticas se denota por $\mathcal {P}(\Omega)$ ) y como función de probabilidad

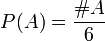
$P(A)= \frac {\# A} {6}$
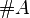donde $\# A$ representa el número de elementos del conjunto

A

.
Es fácil comprobar que esta función verifica los tres axiomas de Kolmogórov y, por tanto, consituye una probabilidad sobre este conjunto.

$P(A)= \frac {\# A} {6} \geq 0$ , puesto que es el cociente de dos números positivos
$P(\Omega)=P \left ( \left \{ 1, 2, 3, 4, 5, 6 \right \} \right )= \frac { \# \left \{ 1, 2, 3, 4, 5, 6 \right \} } {6} = \frac {6} {6} = 1$
Si $A= A_1 \cup A_2 \cup A_3 \cup \cdots$ de tal manera que $A_i \cap A_j = \varnothing \quad \forall i \ne j$ entonces

$\# A = \# A_1 + \# A_2 + \# A_3 + \cdots$

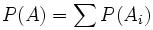
con lo que $P(A)=\sum P(A_i)$

TEOREMAS

TEOREMA 1. Si f es un evento nulo o vacío, entonces la probabilidad de que ocurra f debe ser cero.

A

p(f)=0

DEMOSTRACIÓN:

Si sumamos a fun evento A cualquiera, como f y A son dos eventos mutuamente excluyentes, entonces p(AfÈ)=p(A) +p(f)=p(A). LQQD

TEOREMA 2. La probabilidad del complemento de A, A^c debe ser, p(A^c)= 1 – p(A)

DEMOSTRACIÓN:

Si el espacio muestral d, se divide en dos eventos mutuamente exclusivos, A y A^c luego d=AÈA^c, por tanto p(d)=p(A) + p(A^c) y como en el axioma dos se afirma que p(d)=1, por tanto, p(A^c)= 1 - p(A) .LQQD

TEOREMA 3. Si un evento A Ì B, entonces la p(A) £ p(B).

TECNICAS DE CONTEO

TECNICAS DE CONTEO

Las técnicas de conteo son aquellas que son usadas para enumerar eventos difíciles de cuantificar.

Ejemplos en los que definitivamente haremos uso de las técnicas de conteo serían:

-¿Cuántas comisiones pro limpieza del instituto se pueden formar si hay 150 alumnos que desean ayudar en esta tarea y se desea formar comisiones de ocho alumnos?

-¿Cuántas representaciones de alumnos pueden ser formadas a) si se desea que estas consten solo de alumnos de Ingeniería Química?, b) se desea que el presidente sea un químico?, c) se desea que el presidente y tesorero sean químicos? Para todos los casos, se desea que las representaciones consten de once alumnos.

-¿Cuántas maneras tiene una persona de seleccionar una lavadora, una batidora y dos licuadoras, si encuentra en una tienda 8 modelos diferentes de lavadoras, 5 modelos diferentes de batidoras y 7 modelos diferentes de licuadoras?

Se les denomina técnicas de conteo a: las combinaciones, permutaciones y diagrama de árbol, las que a continuación se explicarán y hay que destacar que éstas nos proporcionan la información de todas las maneras posibles en que ocurre un evento determinado.

Las bases para entender el uso de las técnicas de conteo son el principio multiplicativo y el aditivo, los que a continuación se definen y se hace uso de ellos.

PRINCIPIO MULTIPLICATIVO.

Si se desea realizar una actividad que consta de r pasos, en donde el primer paso de la actividad a realizar puede ser llevado a cabo de N₁ maneras o formas, el segundo paso de N₂ maneras o formas y el r-ésimo paso de N_r maneras o formas, entonces esta actividad puede ser llevada a efecto de;

N₁ x N₂ x ..........x N_r maneras o formas

El principio multiplicativo implica que cada uno de los pasos de la actividad deben ser llevados a efecto, uno tras otro.

Ejemplos:

1) Una persona desea construir su casa, para lo cuál considera que puede construir los cimientos de su casa de cualquiera de dos maneras (concreto o block de cemento), mientras que las paredes las puede hacer de adobe, adobón o ladrillo, el techo puede ser de concreto o lámina galvanizada y por último los acabados los puede realizar de una sola manera ¿cuántas maneras tiene esta persona de construir su casa?

Solución:

Considerando que r = 4 pasos

N₁= maneras de hacer cimientos = 2

N₂= maneras de construir paredes = 3

N₃= maneras de hacer techos = 2

N₄= maneras de hacer acabados = 1

N₁ x N₂ x N₃ x N₄ = 2 x 3 x 2 x 1 = 12 maneras de construir la casa

PERMUTACIONES.

Para entender lo que son las permutaciones es necesario definir lo que es una combinación y lo que es una permutación para establecer su diferencia y de esta manera entender claramente cuando es posible utilizar una combinación y cuando utilizar una permutación al momento de querer cuantificar los elementos de algún evento.

COMBINACIÓN Y PERMUTACION.

COMBINACIÓN:

Es todo arreglo de elementos en donde no nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.

PERMUTACIÓN:

Es todo arreglo de elementos en donde nos interesa el lugar o posición que ocupa cada uno de los elementos que constituyen dicho arreglo.

Para ver de una manera objetiva la diferencia entre una combinación y una permutación, plantearemos cierta situación.

Suponga que un salón de clase está constituido por 35 alumnos. a) El maestro desea que tres de los alumnos lo ayuden en actividades tales como mantener el aula limpia o entregar material a los alumnos cuando así sea necesario.

b) El maestro desea que se nombre a los representantes del salón (Presidente, Secretario y Tesorero).

Solución:

a) Suponga que por unanimidad se ha elegido a Daniel, Arturo y a Rafael para limpiar el aula o entregar material, (aunque pudieron haberse seleccionado a Rafael, Daniel y a Enrique, o pudo haberse formado cualquier grupo de tres personas para realizar las actividades mencionadas anteriormente).

¿Es importante el orden como se selecciona a los elementos que forma el grupo de tres personas?

Reflexionando al respecto nos damos cuenta de que el orden en este caso no tiene importancia, ya que lo único que nos interesaría es el contenido de cada grupo, dicho de otra forma, ¿quiénes están en el grupo? Por tanto, este ejemplo es una combinación, quiere decir esto que las combinaciones nos permiten formar grupos o muestras de elementos en donde lo único que nos interesa es el contenido de los mismos.

b) Suponga que se han nombrado como representantes del salón a Daniel como Presidente, a Arturo como secretario y a Rafael como tesorero, pero resulta que a alguien se le ocurre hacer algunos cambios, los que se muestran a continuación:

CAMBIOS

PRESIDENTE:	Daniel	Arturo	Rafael	Daniel
SECRETARIO:	Arturo	Daniel	Daniel	Rafael
TESORERO:	Rafael	Rafael	Arturo	Arturo

Ahora tenemos cuatro arreglos, ¿se trata de la misma representación?

Creo que la respuesta sería no, ya que el cambio de función que se hace a los integrantes de la representación original hace que definitivamente cada una de las representaciones trabaje de manera diferente, ¿importa el orden de los elementos en los arreglos?. La respuesta definitivamente sería sí, luego entonces las representaciones antes definidas son diferentes ya que el orden o la forma en que se asignan las funciones sí importa, por lo tanto es este caso estamos tratando con permutaciones.

PERMUTACIONES CON REPETICION.

En los casos anteriores se han obtenido permutaciones en donde todos los elementos utilizados para hacer los arreglos son diferentes. A continuación se obtendrá una fórmula que nos permite obtener las permutaciones de n objetos, cuando entre esos objetos hay algunos que son iguales.

Ejemplo:

Obtenga todas las permutaciones posibles a obtener con las letras de la palabra OSO.

Solución:

Para obtener la fórmula, es necesario primero suponer que todas las letras de la palabra OSO son diferentes y para diferenciarlas pondremos subíndices a las letras O, por lo que quedaría, O₁SO_2,y las permutaciones a obtener serían:

₃P₃ = 3! = 6

definiendo las permutaciones tenemos que estas serían,

O₁SO₂, O₂SO₁, SO₁O₂, SO₂O₁, O₁O₂S, O₂O₁S

¿Pero realmente podemos hacer diferentes a las letras O?, eso no es posible, luego entonces ¿cuántos arreglos reales se tienen?

Como:

Arreglos reales

O₁SO₂ = O₂SO₁® OSO

SO₁O₂ = SO₂O₁® SOO

O₁O₂S= O₂O₁S ® OOS

Entonces se observa que en realidad sólo es posible obtener tres permutaciones con las letras de la palabra OSO debido a que las letras O son idénticas, ¿pero qué es lo que nos hizo pensar en seis arreglos en lugar de tres?, el cambio que hicimos entre las letras O cuando las consideramos diferentes, cuando en realidad son iguales.

Para obtener los arreglos reales es necesario partir de la siguiente expresión:

El número de arreglos reales = No. de permutaciones considerando a todos los objetos como diferentes

Los cambios entre objetos iguales

El número de arreglos reales = 3! / 2! = 3 x 2! / 2! = 3

Por tanto la fórmula a utilizar sería;

Donde:

nPx₁,x₂,......, x_k = Número total de permutaciones que es posible obtener con n objetos, entre los que hay una cantidad x₁ de objetos de cierto tipo, una cantidad x₂ de objetos de un segundo tipo,...... y una cantidad x_k de objetos del tipo k.

n = x₁ + x₂ + ...... + x_k

Ejemplos:

1) Obtenga todas las señales posibles que se pueden diseñar con seis banderines, dos de los cuales son rojos, tres son verdes y uno morado.

Solución:

n = 6 banderines

x₁ = 2 banderines rojos

x₂= 3 banderines verdes

x₃ = 1 banderín morado

₆P₂,₃,₁ = 6! / 2!3!1! = 60 señales diferentes

COMBINACIONES.

Como ya se mencionó anteriormente, una combinación, es un arreglo de elementos en donde no nos interesa el lugar o posición que ocupan los mismos dentro del arreglo. En una combinación nos interesa formar grupos y el contenido de los mismos.

La fórmula para determinar el número de combinaciones es:

_nC_r = Combinaciones de r objetos tomados de entre n objetos

Donde se observa que,

La expresión anterior nos explica como las combinaciones de r objetos tomados de entre n objetos pueden ser obtenidas a partir de las permutaciones de r objetos tomados de entre n objetos, esto se debe a que como en las combinaciones no nos importa el orden de los objetos, entonces si tenemos las permutaciones de esos objetos al dividirlas entre r!, les estamos quitando el orden y por tanto transformándolas en combinaciones, de otra forma, también si deseamos calcular permutaciones y tenemos las combinaciones, simplemente con multiplicar estas por el r! obtendremos las permutaciones requeridas.

_nP_r = _nC_r r!

Y si deseamos r = n entonces;

_nC_n = n! / (n –n)!n! = n! / 0!n! = 1

¿Qué nos indica lo anterior?

Que cuando se desea formar grupos con la misma cantidad de elementos con que se cuenta solo es posible formar un grupo.

Ejemplos:

1) a. Si se cuenta con 14 alumnos que desean colaborar en una campaña pro limpieza del Tec, cuantos grupos de limpieza podrán formarse si se desea que consten de 5 alumnos cada uno de ellos, b.si entre los 14 alumnos hay 8 mujeres, ¿cuantos de los grupos de limpieza tendrán a 3 mujeres?, c.¿cuántos de los grupos de limpieza contarán con 4 hombres por lo menos?

Solución:

a. n = 14, r = 5

₁₄C₅= 14! / (14 – 5 )!5! = 14! / 9!5!

= 14 x 13 x 12 x 11 x 10 x 9!/ 9!5!

= 2002 grupos

DIAGRAMA DE ARBOL.

Un diagrama de árbol es una representación gráfica de un experimento que consta de r pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo.

Un diagrama de árbol es una representación gráfica que muestra los resultados posibles de una serie de experimentos y sus respectivas probabilidades.

1) Experimento: Se lanza una moneda, si sale águila se lanza un dado y si sale sol se lanza la moneda de nuevo.

Espacio muestral
S:{A1,A2,A3,A4,A5,A6,SS,SA}
n(s)=8

2)Experimento: Suponga que de un proceso de fabricación se seleccionan tres artículos de forma aleatoria. Cada articulo se inspecciona se clasifica como defectuoso o no defectuoso.

S={DDD, DDN,DND,DNN,NDD,NND,NNN}

n(s)=8

3)Experimento: Se tienen tres pelotas en una bolsa de color blanco, azul y amarillo, si se saca una pelota pero no se regresa y se vuelve a sacar otra. ¿Cuál sera el espacio muestral?

S={RB,RA,BR,BA,AR,AB}
n(s)=6

EXPERIMENTO,SUCESO,ESPACIO MUESTRAL, ENTRE OTROS.

EXPERIMENTO:

Un experimento, en estadística, es cualquier proceso que proporciona datos, numéricos o no numéricos.

ESPACIO MUESTRAL:

Un conjunto cuyos elementos representan todos los posibles resultados de un experimento se llama espacio muestral y se representa como S. El espacio muestral de un experimento siempre existe y no es necesariamente único pues, dependiendo de nuestra valoración de los resultados, podemos construir diferentes espacios muestrales.

Los elementos del espacio muestral se llaman puntos muestrales y son los distintos resultados del experimento.

SUCESO:

Si consideramos el conjunto de las partes de (P(S)) sus elementos son los sucesos. Un

suceso, por tanto, es un subconjunto del espacio muestral.

LOS TIPOS DE SUCESOS:

· Sucesos simples:, que son aquellos que comprenden un sólo punto muestral.

· Sucesos compuestos;, que son los que engloban más de un punto del espacio muestral. Todo suceso compuesto se puede considerar como unión de puntos del espacio muestral o unión de sucesos simples.

Azar, suceso aleatorio y probabilidad.

El azar, en el lenguaje normal, se considera como la característica de un suceso imprevisible.

En estadística esta definición se modifica añadiendo una propiedad adicional: El azar es la característica de un experimento que produce resultados diversos, impredecibles en cada situación concreta, pero cuyas frecuencias, a la larga, tienden a estabilizarse hacia un valor "límite" en el infinito.

Como consecuencia, se definen los sucesos aleatorios como los resultados de un experimento cuya variación (la de los resultados) es debida al azar.

La probabilidad de un suceso sólo se define para el caso de sucesos aleatorios.

Hay varias formas de definir la probabilidad.

En primer lugar podemos considerar la definición intuitiva que nos dice que la probabilidad de un suceso es la posibilidad de que éste ocurra. Esta primera definición no parece de gran utilidad por ser difícilmente cuantificable.

También podemos considerar la definición clásica de probabilidad. En esta definición se empieza por considerar todos los resultados posibles de un experimento; después se contabilizan los resultados favorables a nuestro suceso, es decir, todos aquellos en que el experimento resulta en el suceso considerado; por último, suponiendo que existe simetría recíproca de todos los resultados, es decir, que todos los resultados posibles son igualmente posibles, se define la probabilidad como el número de casos favorables dividido por el número de casos posibles.

Esta segunda definición presenta el inconveniente de que no siempre es posible saber cuantos son los resultados posibles de un experimento y no siempre todos los resultados posibles son igualmente probables.

Por tanto, consideraremos la probabilidad definida de otra forma. Supongamos que realizamos muchas veces un experimento y vamos anotando el valor de la frecuencia relativa que, como sabemos, tiende a estabilizarse. Suponiendo que pudiéramos realizar el experimento infinitas veces, el valor de estabilización de las frecuencias en el infinito sería la probabilidad de los sucesos. Es decir, la probabilidad es el valor de la frecuencia relativa en el infinito. Es importante señalar, que este valor de estabilización no es un límite en el sentido matemático de la expresión pues, por ser un suceso aleatorio, nadie puede garantizar una ecuación matemática para el valor de la frecuencia relativa.

Todo el cálculo de probabilidades y, con él, toda la estadística se basan en tres propiedades que se asignan a las probabilidades, que se llaman axiomas de Kolmogorov

1. La probabilidad de un suceso es siempre mayor o igual que cero y menor o igual que uno

Si A es un suceso

2. La probabilidad del espacio muestral es igual a uno:

Si S es el espacio muestral

Es evidente, pues si realizamos un experimento siempre a de suceder alguna cosa. Esta propiedad se expresa como que la probabilidad de un suceso cierto es igual a uno. Si S tiene un único elemento ése es un suceso cierto. Como consecuencia, siguiendo el razonamiento anterior, la probabilidad de que no ocurra nada, lo cual es imposible, o en notación de conjuntos la probabilidad del conjunto vacío (F) es cero. P(F) = 0

Se llama suceso imposible a aquel cuya probabilidad vale cero.

3. Si A y B son sucesos mutuamente excluyentes, es decir, nunca ocurren simultáneamente (A Ç B = F) la probabilidad de su unión, es decir, de que ocurra uno u otro es la suma de sus probabilidades.

P(A È B) = P(A) + P(B)

Otras propiedades de las probabilidades.

· Si A y B son dos sucesos cualesquiera:

· Se llama suceso contrario del suceso A al suceso A' que se define como

A’ = S – A. La probabilidad del suceso contrario es:

· Se llama probabilidad condicional del suceso B respecto del suceso A a la probabilidad de que, dado que el resultado de un experimento haya sido A sea, simultáneamente, B. Este valor se representa como P(B|A).

Por transposición de términos en la ecuación anterior y en la correspondiente a la probabilidad condicional de A respecto de B llegamos a:

· Se dice que dos sucesos A y B son independientes si y sólo si la probabilidad de su intersección es igual al producto de sus probabilidades


Sucesos dependientes	Sucesos independientes

Variables aleatorias

Como dijimos, un experimento estadístico es cualquier proceso que proporciona datos. Para su utilización en estadística, estos datos tienen que despojarse de detalles accesorios para convertirse en descripciones numéricas del resultado; la utilización de clasificaciones cualitativas, restringe a la mera descripción las posibilidades de manejo estadístico.

Estas descripciones numéricas son observaciones aleatorias. A las observaciones aleatorias se les considera como la expresión en cada caso concreto de una variable aleatoria que toma valores en los resultados del experimento.

Así pues, una variable aleatoria es una función cuyos valores son números reales determinados por los elementos del espacio muestral, es decir, una variable aleatoria es una variable matemática cuyos valores posibles son las descripciones numéricas de todos los resultados posibles de un experimento estadístico.

A los valores posibles de la variable aleatoria se les asigna una probabilidad que es la frecuencia del resultado al que corresponden.

Se pueden distinguir distintos tipos de variables aleatorias según dos criterios de clasificación:

1. Variables cuantitativas que son las que resultan de experimentos cuyos resultados son directamente numéricos.

2. Variables cualitativas que son las que proceden de experimentos cuyos resultados expresan una cualidad no numérica que necesita ser cuantificada.

Otra clasificación más operativa de las variables aleatorias sería:

A. Variable discreta: Aquella que se define sobre un espacio muestral numerable, finito o infinito. Espacio numerable es aquel cuyos elementos se pueden ordenar, asignándoles a cada uno un número de la serie de los números naturales (del 1 al n ó del 1 al I). Todas las variables con un número finito de valores y todas las que tomen valores en números enteros o racionales (fraccionarios), son variables discretas.

B. Variable continua: Es aquella que se define sobre un espacio asimilable al conjunto de los números reales, es decir, un espacio no numerable (o un espacio infinito de tipo C o infinito dos)

En general, la regla de oro es que todas las variables que proceden de experimentos en los que se cuenta son discretas y todas las variables que proceden de experimentos en los que se mide son continuas.

Variables aleatorias discretas

Función de probabilidad

Una variable aleatoria discreta toma cada uno de sus valores con una determinada probabilidad.

La relación entre valores y probabilidades en una variable X se puede expresar de forma tabular de la siguiente manera:

Valores de X	x₁	x₂	...	x_i
P(X = x)	P(x₁)	P(x₂)		P(x_i)

Este método puede ser complicado, e incluso imposible, si los valores de la variable son muchos o infinitos.

En algunos casos, existe una forma sistemática de aplicación de los valores de la probabilidad a los valores de la variable, de modo tal que se puede establecer una ecuación que ligue ambos. A esta ecuación se le llama función de probabilidad. Por tanto, la función de probabilidad de una variable aleatoria discreta X es una función tal que, al sustituir x por un valor de la variable, el valor que toma la función es la probabilidad de que la variable X asuma el valor x. Habitualmente, la función de probabilidad se representa como f(x).

f(x) = P(X = x)

Las funciones de probabilidad sólo se definen para los valores de la variable aleatoria y deben cumplir tres propiedades:

Como consecuencia del primer axioma.

Como consecuencia del segundo axioma.

3. P(X = x) = f(x) Por definición.

TEORIA DE CONJUNTOS

LA TEORÍA DE CONJUNTOS

Rama de las matemáticas a las que el matemático Georg Ferdinand Ludwing Philipp Cantor es el padre de la Teoría de Conjuntos, dio su primer tratamiento formal en 1870. El concepto de conjunto es uno de los más fundamentales en matemáticas, incluso más que la operación de contar, pues se puede encontrar implícita o explícitamente, en todas las ramas de las matemáticas puras y aplicadas. En su forma explícita, los principios y terminología de los conjuntos se utilizan para construir proposiciones matemáticas más claras y precisas y para explicar conceptos abstractos como el infinito.

En el año 1874, apareció el primer trabajo revolucionario de Cantor sobre la Teoría de conjuntos.

QUE ES UN CONJUNTO

Sabemos que la palabra conjunto implica la idea de una colección de objetos que se caracterizan en algo común.

En matemática tiene el mismo significado, sólo que a estos objetos se les llama elementos o miembros del conjunto.

La noción simple de una colección o conjunto de objetos es fundamental en la estructura básica de las matemáticas y fue Georg Cantor, en los años 1870 quien primero llamó la atención de los matemáticos a este respecto.

No puede darse una definición satisfactoria de un conjunto en términos de conceptos simples, por lo tanto la palabra "CONJUNTO" debe aceptarse lógicamente como un término no definido.

Un conjunto es una colección bien definida de objetos de cualquier clase.

DETERMINACIÓN DE UN CONJUNTO

Hay dos formas de determinar conjuntos.

ó Forma Tabular

Se dice que un conjunto es determinado por extensión (o enumeración), cuando se da una lista que comprende a todos los elementos del conjunto y sólo a ellos.

A = { a, e, i, o, u }

B = { 0, 2, 4, 6, 8 }

C = { c,

, j, u, t, s } En un conjunto determinado por extensión no se repite un mismo elemento.

ó Forma Constructiva

Se dice que un conjunto es determinado por comprensión, cuando se da una propiedad que la cumpla en todos los elementos del conjunto y sólo a ellos.

A = { x/x es una vocal }

B = { x/x es un número par menor que 10 }

C = { x/x es una letra de la palabra conjuntos }

Vamos a mostrarte un cuadro comparativo de determinación de conjuntos

A = { a, e, i, o, u }

A = { x/x es una vocal }

B = { 0, 2, 4, 6, 8 }

B = { x/x es un número par menor que 10 }

C = { c,

, j, u, t, s }

C = { x/x es una letra de la palabra conjuntos }

D = { 1, 3, 5, 7, 9 }

D = { x/x es un número impar menor que 10 }

E = { b, c, d, f, g, h, j, . . . }

E = { x/x es una consonante }

POR DIAGRAMA DE VENN O FORMA GRAFICA

A cada conjunto se le considera encerrado dentro de una curva (plana) cerrada. Los elementos del conjunto considerado pueden ser específicamente dibujados o pueden quedar (implícitamente) sobreentendidos. Los diagramas son empleados, para representar tanto a los conjuntos como a sus operaciones, y constituyen una poderosa herramienta geométrica, desprovista de validez lógica.

A continuación representaremos algunos conjuntos y verificaremos algunas igualdades (las intersecciones de dos o más conjuntos quedan caracterizados por el rayado múltiple).

El gráfico es la representación de la unión

El gráfico es la representación de la intersección

El gráfico es la representación de la diferencia

CLASES DE CONJUNTOS

CONJUNTOS FINITOS

Un conjunto es finito si consta de un cierto número de elementos distintos, es decir si al contar los diferentes elementos del conjunto el proceso de contar puede acabar. En caso contrario, el conjunto es infinito.

M = { x / x es un río de la tierra } Conjunto finito

N = { 0, 1, 2, 3, 4, 5, 6, 7, 8, ... } Conjunto infinito

P = { x / x es un país de la tierra } Conjunto finito

V = { 3, 6, 9, 12, 15, 18, 21, 24, 27, ... } Conjunto infinito

IGUALDAD DE CONJUNTOS

Se dice que 2 conjuntos A y B son iguales cuando ambos tienen los mismos elementos, es decir si cada elemento de A pertenece a B y si cada elemento que pertenece a B pertenece también a A. La igualdad se denota A = B.

En la igualdad, el orden de los elementos de cada conjunto no importa.

A = {1, 2, 3, 4}

C = {1, 2, 3, 3, 4, 1}

E = {vocal de la palabra mundo}

B = {3, 4, 1, 2}

D = {1, 2, 2, 3, 4, 4,}

F = {u, o}

A = B

C = D

E = F

CONJUNTO VACÍO

Es un conjunto que carece de elementos. Se suele llamarle conjunto nulo, y se le denota por el símbolo ø o { }.

A = { Los perros que vuelan }	A = { }	A = Ø
B = { x / xes un mes que tiene 53 días}	B = { }	B = Ø
C = { x / x³ = 8 y x es impar }	C = { }	C = Ø
D = { x / xes un día de 90 horas }	D = { }	D = Ø

CONJUNTO UNITARIO

Es todo conjunto que está formado por un sólo y único elemento.

A = { 5 }

B = {números pares entre 6 y 10} = { 8 }

C = {la capital del Perú } = { Lima }

D = {x / 2x = 6} = {3}

CONJUNTO UNIVERSAL

Es el conjunto que contiene a todos los elementos del discurso. Es un término relativo. Se le denota por la letra U.

Sean los conjuntos:

A = { aves }

B = { peces }

C = { conejos }

D = { monos }

Existe otro conjunto que incluye a los conjuntos A, B, C y D. Es

U = { animales }

Gráficamente se representa por un rectángulo tal como se observa a continuación.

Representación gráfica de un conjunto universal

Sean los conjuntos:

E = { mujeres }

F = { hombres }

Existe otro conjunto que incluye a los conjuntos E y F. Es

U = { seres humanos }

Gráficamente se representa por un rectángulo tal como se observa a continuación.

CONJUNTO POTENCIA

La familia de todos los subconjuntos de un conjunto M se llama Conjunto Potencia de M. Se le denota como 2^M .

a)	M = { 1, 2 }	El conjunto M tiene 2 elementos
	2^M = { {1}, {2}, {1, 2}, ø}	entonces 2² = 4 elementos

b)	M = { 1, 2, 3 }	El conjunto M tiene 3 elementos
	2^M = { {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}, ø}	entonces 2³= 8 elementos

Si un conjunto M es finito con "n" elementos, entonces su conjunto potencia 2^M tendrá 2ⁿ elementos.

CONJUNTOS DISJUNTOS

Si dos conjuntos A y B no tienen ningún elemento común entonces A y B son disjuntos.

Conjuntos disjuntos				Conjuntos no disjuntos

A = { 2, 4, 6 }				M = { o, p, q, r, s }
B = { 1, 3, 5 }				N = { s, t, v, u }
A y B son disjuntos.				M y N no son disjuntos.

C = { x/x es una letra del alfabeto }				P = { x/x es una letra de la palabra aritmética }
D = { x/x es un número }				Q = { x/x es una letra de la palabra algebra }
C y D son disjuntos				P y Q no son disjuntos

FORMAS DE REPRESENTAR UN CONJUNTO

UNIÓN DE CONJUNTOS

La unión de los conjuntos A y B es el conjunto formado por todos los elementos que pertenecen a A o a B o a ambos. Se denota: A U B. La unión de conjuntos se define como:

A U B = {x / x

A o x

En forma gráfica:


Cuando no tienen	Cuando tienen algunos	Cuando todos los elementos de un
elementos comunes	elementos comunes	conjunto pertenecen a otro conjunto

1. Dados los conjuntos: A = { 0, 1, 2, 3, 4, 5 }, B = { 0, 2, 4 } y C = { 5, 6, 8 }, efectuar y construir los diagramas respectivos:

A U C

B U C

A U B

Tenemos:

a) A = { 0, 1, 2, 3, 4, 5 } y C = { 5, 6, 8 }

						A U C = { 0, 1, 2, 3, 4, , 6, 8 }

						Representación gráfica de la unión de conjuntos A y C

INTERSECCIÓN DE CONJUNTO

Se define la intersección de dos conjuntos A y B al conjunto de elementos que son comunes a A y B. Se denota por A

B, que se lee: A intersección B. La intersección de A y B también se puede definir:

B = { x / x

A y x

B } y mediante un diagrama de Venn-Euler:


Cuando tienen	Cuando no tienen	Cuando todos los elementos de un
elementos comunes	elementos comunes	conjunto pertenecen a otro conjunto

1. Dados los conjuntos: A = { 0, 1, 2, 3, 4, 5 }, B = { 3, 5, 7 } y C = { 2, 4 }, efectuar y construir los diagramas respectivos:

A C

B C

A B

Tenemos:

a) A = { 0, 1, 2, 3, 4, 5 } y C = { 2, 4 }

				A C = { , }

				Representación gráfica de la intersección de conjuntos A y C

DIFERENCIA DE CONJUNTOS

Se denomina diferencia de dos conjuntos A y B al conjunto formado por todos los elementos de A pero que no pertenecen a B.

La diferencia se denota por: A - B que se lee: A diferencia B o A menos B. Se define la diferencia de dos conjuntos también como:

A - B = {x / x

A y x

Mediante un diagrama de Venn - Euler:


Cuando no tienen	Cuando tienen	Cuando todos los elementos de un
elementos comunes	elementos comunes	conjunto pertenecen a otro conjunto

1. Dados los conjuntos: A = { a, b, c, d, e }, B = { a, e } y C = { d, f, g }, efectuar y construir los diagramas respectivos:

A - C

B - C

A - B

Tenemos:

a) A = { a, b, c, d, e } y C = { d, f, g }

				A - C = { a, b, c, e }

				Representación gráfica de la diferencia de conjuntos A y C

COMPLEMENTO DE UN CONJUNTO

Si un conjunto A es subconjunto de otro conjunto universal U, al conjunto A' formado por todos los elementos de U pero no de A, se llama complemento de A con respecto a U. Simbólicamente se expresa:

A' = { x/x

U y x

A }

a)	Sean U = { m, a, r, t, e }		y		A = { t, e }
	Su complemento de A es:				A' = { m, a, r }

	En forma gráfica:

b)	Sean U = { letras de la palabra aritmética}	y	B = { vocales de la palabra vida }
	Determinado por extensión tenemos
	U = { a, r, i, t, m, e, c }		B = { i, a }
	Su complemento de B es:		B' = { r, t, m, e, c }

	En forma gráfica:

EJERCICIOS CON SUS RESPECTIVAS RESPUESTAS

EJERCICIOS DE CONJUNTOS

Preguntas

1)		Cuáles son los elementos de:
	a)	El conjunto de los dias de la semana
	b)	El conjunto de las estaciones del año
	c)	Los números impares menores de 11
	d)	Los números pares mayor que 10 y menor que 20
	e)	Los números primos menores de 15

2)		Colocar V ó F según lo afirmado sean verdadero o falso
	a)	6 { 2, 4, 5, 6, 9 }	( )
	b)	y { o, p, q, x }	( )
	c)	x { o, p, q, y }	( )
	d)	Perú { países de Europa }	( )
	e)	Amazonas { rios de América }	( )

3)		¿Cuáles de los siguientes conjuntos son: vacios, unitarios, finitos, infinitos?
	a)	A = { x / x es día de la semana}	. . . . .
	b)	B = { vocales de la palabra vals}	. . . . .
	c)	C = { 1, 3, 5, 7, 9, . . . . .}	. . . . .
	d)	D = { x / x es un habitante de la luna}	. . . . .
	e)	E = { x N / x < 15}	. . . . .
	f)	F = { x N y 5 < x < 5 }	. . . . .
	g)	G = { x N y x > 15}	. . . . .
	h)	H = { x N y x = x}	. . . . .
	i)	I = { x / x es presidente del Oceano Pacífico}	. . . . .
	j)	J = { x / x es número de cabellos total de los habitantes del Perú }	. . . . .

RESPUESTA DE EJERCICIOS DE CONJUNTOS

1)		Cuáles son los elementos de:
	a)	A = {lunes, martes, miércoles, jueves, viernes, sábado, domingo }
	b)	B = {verano, otoño, invierno, primavera }
	c)	C = {1, 3, 5, 7, 9 }
	d)	D = {12, 14, 16, 18 }
	e)	E = {1, 2, 3, 5, 7, 11, 13 }

2)		Colocar V ó F según lo afirmado sean verdadero o falso
	a)	6 { 2, 4, 5, 6, 9 }	( V )
	b)	y { o, p, q, x }	( F )
	c)	x { o, p, q, y }	( V )
	d)	Perú { países de Europa }	( F )
	e)	Amazonas { rios de América }	( F )

3)		¿Cuáles de los siguientes conjuntos son: vacios, unitarios, finitos, infinitos?
	a)	A = { x / x es día de la semana}	finito
	b)	B = { vocales de la palabra vals}	unitario
	c)	C = { 1, 3, 5, 7, 9, . . . . .}	infinito
	d)	D = { x / x es un habitante de la luna}	vacio
	e)	E = { x N / x < 15}	finito
	f)	F = { x N y 5 < x < 5 }	vacio
	g)	G = { x N y x > 15}	infinito
	h)	H = { x N y x = x}	unitario
	i)	I = { x / x es presidente del Oceano Pacífico}	vacio
	j)	J = { x / x es número de cabellos total de los habitantes del Perú }	infinito